Milwaukee Art Museum-Bird

Aufstellen der Fächengleichung und Herleitung geometrischer Eigenschaften

> restart;

Der Richtungsvektor der Leitgeraden sei (p,q), dann ist jede Normalebene gegeben durch:

> N:=p*y+q*z+d;

d hängt dann vom Punkt der Leitkurve ab, durch den die Normalebene durchgehen soll

Die Leitkurve sei eine Ellipse mit der Parameterdarstellung x=a*cos(t), y=b*sin(t)

> NN:=subs(y=b*sin(t),z=0,N);

> d:=solve(%,d);

> g:=-q*y+p*z;

Damit ist die Normalebene festgelegt. Wir schneiden sie mit der Leitgeraden

> solve({g,N},{y,z});

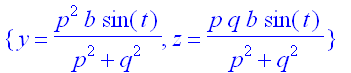
> Ny:=op(2,%[1]);Nz:=op(2,%%[2]);

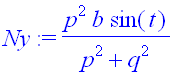
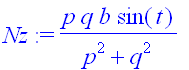
Damit ist die Flächengleichung festgelegt

> FL:=[a*cos(t)+lambda*a*cos(t),b*sin(t)+lambda*(b*sin(t)-Ny),-lambda*Nz];

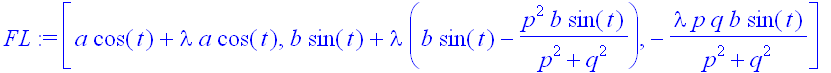
Plot eines Beispiels:

> FL1:=subs(a=2,b=4,p=3,q=2,FL);

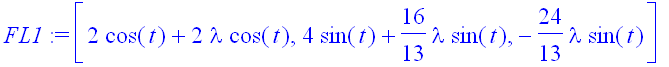
> with(plots):

Warning, the name changecoords has been redefined

Wir plotten die Leitellipse, die Leitgerade und die Fläche

> lg:=spacecurve([0,3*t,2*t],t=-1..1,thickness=4,color=black):

> lk:=spacecurve([2*cos(t),4*sin(t),0],t=0..2*Pi,thickness=4,color=red):

> F:=plot3d(FL1,t=0..2*Pi, lambda=-2..1):

> display3d(F,lk,lg,axes=framed,scaling=constrained,orientation=[40,70]);

Calatrava verwendet nur einen Teil dieser Fläche:

> lg:=spacecurve([0,3*t,2*t],t=-1..1,thickness=4,color=black):

> lk:=spacecurve([2*cos(t),4*sin(t),0],t=0..2*Pi,thickness=4,color=red):

> F:=plot3d(FL1,t=0..Pi, lambda=-1..0):

> display3d(F,lk,lg,axes=framed,scaling=unconstrained,orientation=[40,70]);

Ermittlung der algebraischen Flächengleichung

> FL;

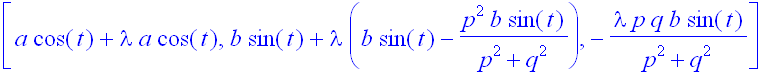
> g1:=FL[1]-X;

> g2:=FL[2]-Y;

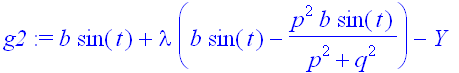
> g3:=FL[3]-Z;

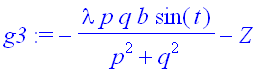
Elimination der Parameter aus der Flächengleichung

> solve(g1,lambda);

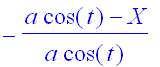
> lambda:=%;

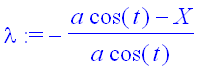
> G2:=factor(subs(cos(t)=(1-u^2)/(1+u^2),sin(t)=2*u/(1+u^2),g2));

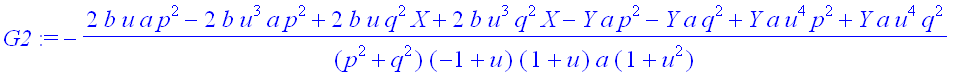
> G3:=factor(subs(cos(t)=(1-u^2)/(1+u^2),sin(t)=2*u/(1+u^2),g3));

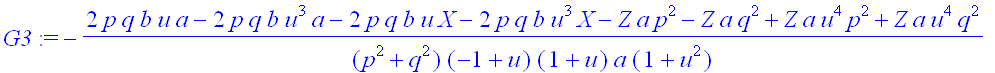
> G2:=numer(G2);

> G3:=numer(G3);

> factor(resultant(G2,G3,u));

> RF:=op(8,%);

Daraus folgt: Die Fläche ist ein gerades Konoid von der Ordnung 4.

Berechnung der Fernkurve:

> factor(subs(X=x1/x0,Y=x2/x0,Z=x3/x0,RF));

> numer(%);

> subs(x0=0,%);

> factor(%);

Daraus folgt: Die Ferngerade der Leitebene ist eine Doppelgerade und der Restschnitt ist ein Kegelschnitt

Da wir nun schon zwei Doppelleitgeraden kennen muss die Doppelkurve - die bei einer RF vom Grad vier eine Kubik sein muss - in drei Geraden zerfallen. Wir können die Doppelkurve als Nullstellen der vier Gleichungen RF=0, dRF/dX=0,dRF/dY=0, dRF/dZ=0 berechnen

> RFx:=diff(RF,X);

> RFy:=diff(RF,Y);

> RFz:=diff(RF,Z);

> factor(resultant(RFx,RFy,X));

> factor(resultant(RFx,RFz,X));

In den beiden Gleichungen sieht man zwei gleiche Faktoren: diese gehören zu den beiden eigentlichen Doppelgeraden:

der erste Faktor ist genau die vorgegebene Leitgerade (X=0, Z*p-q*Y=0) und der zweite Faktor ist die X-Achse

> factor(subs(Z=-q/p*Y,RFx));

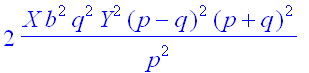
> factor(subs(Z=0,Y=0,RF));

Die Fläche enthält daher zwei Leitgeraden und eine Doppelgerade. Sie ist daher eine RF vom Grad vier und VII. Sturmscher Art. Sie ist eine Netzfläche (sie gehört einem hyperbolischen Netz an, Netzgeraden sind die beiden Leitgeraden). Jeder Schnitt durch die Doppelgerade liefert die Doppelgerade und einen Kegelschnitt. Je zwei solcher Schnitte sind projektiv aufeinander bezogen. (Literatur dazu: E. Müller Vorlesungen über Darstellende Geometrie, Band III Konstruktive Behandlung der Regelflächen, bearbeitet von J. Krames, 1931)